The numerics of brain and soft-tissue pathology

Disease and pathology progression are coupled to their environment. The porous environment of soft tissues can be geometrically complex, permeated my multiple fluid networks and described by mechanical coefficients that take on extreme values. Nevertheless, pathology in soft tissues, such as the brain and bowel, pose significant health risks that must be addressed. How can we pose, and solve, mathematical models of pathology and treatment in these challenging environments?
A discontinuous Galerkin method for modeling edema in the small bowel
Brief synopsis
Edema refers to a condition whereby excess fluid accumulates in the spaces between cells. In the small bowel, edema can lead to a disruption of peristalsis, called ileus, that obstructs the movement of biomaterial through both mechanical and neurological means. Fluid resuscitation can restore proper function but testing new fluid resuscitation agents is costly.
What I am doing
I analyzed the stability and convergence of two discontinuous Galerkin finite element methods for a mixed formulation of Biot's equation with a pressure-dependent (Starling) source. I applied the method to model the potential resuscitation benefits of 7.5% hypertonic saline solution. My model indicates (movie, left) that acute edema can cause ileus, by interrupting neuronal signaling (neuropathy) and by lumenal obstruction of the bowel. I also found that 7.5% hypertonic saline may indeed restore normal function.Mixed finite element methods for generalized poroelasticity
Brief synopsis
Soft tissues, such as the human brain, can often be considered as linearly elastic porous media permeated by several fluid networks. This means that they can be modeled by the equations of generalized poroelasticity. The brain, however, is nearly incompressible, nearly impermeable and has a large and complex geometry. Thus, efficiently solving the generalized poroelastic equations, for human brain models, requires special finite element approaches.
What I am doing
The equations of generalized poroelasticity are challenging for nearly incompressible or nearly impermeable porous media such as the brain. In these cases, the stability of typical formulations can depend on the parameters; in the 3-field case, dual Stokes and Darcy stability has been suggested for nearly impermeable media. However, robust Darcy stability is only guaranteed in tricky interpolation spaces and I showed that Darcy stability is not necessary for robust convergence; thus broadening discretization options in practice. To solve model equations on large and complex human brain geometries (image, right), I have engaged in designing block diagonal preconditioners for the nearly incompressible multifluid case and am currently working on a posteriori error estimation and adaptive refinement for generalized poroelastic media.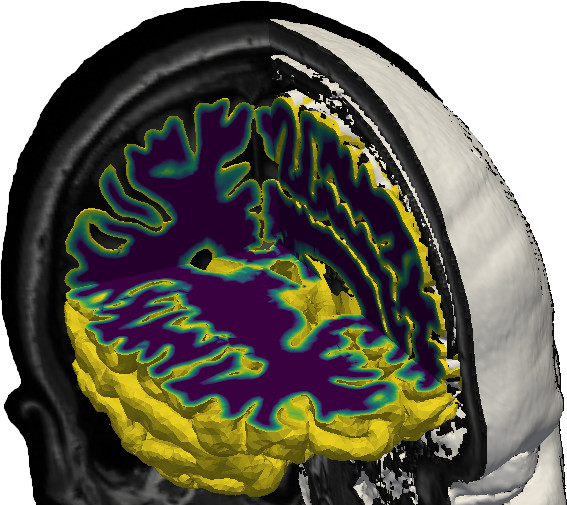
Whole-brain mathematical models from patient imaging data
Brief synopsis
Finite element methods are an important means of modeling human brain and soft tissue mechanics and pathology. The geometry of the brain is complex and diffusion within the brain is highly anisotropic; moreover, these attributes can vary substantially between patients. Patient neuorimaging data is easy to obtain. However, it is not clear how this data can be transformed into the simplicial meshes and tensor information needed to solve poroelastic type mathematical models with finite element approaches.
What I am doing
Alongside colleagues at Simula research laboratory, I have produced a book (Springer, In Press. 2021) describing the step-by-step process of constructing patient volume meshes (movie, left) from neuroimaging data. The extraction of the brain's extracellular diffusion tensor is also detailed. The book demonstrates how these computational assets can be used, together, with FEniCS to produce high-performance, patient specific mathematical model simulations of the whole human brain. An advanced copy of the book, with source code, is available online.